Mecánica de materiales
lunes, 5 de diciembre de 2011
martes, 29 de noviembre de 2011
Calculo de momentos de inercia en ejes de Macizo y Huecos
El momento de inercia de un sólido es una magnitud escalar que viene dada por:
 |
De su definición se deduce que el momento de inercia de un sólido depende del eje de giro (puesto que el radio de giro de cada partícula depende del eje). Como un sólido está constituido por un número muy grande de partículas, en vez de tratarlo como un sistema discreto puede ser analizado como un sistema continuo. Por tanto, el sumatorio de la ecuación anterior puede ser sustituido por la siguiente integral:
 |
Donde dm es un elemento de masa del sólido y R2 su distancia al aje de giro del mismo.
El elemento de masa dm está relacionado con la densidad ρ del sólido y, si éste es homogéneo, al sustituir dm en la expresión del momento de inercia podemos sacar la densidad de la integral:
 |  |
dV es un elemento de volumen del sólido y, para calcular el momento de inercia de un sólido homogéneo es preciso resolver la integral recuadrada en rojo.
Calculos de momentos de inercia:
Como ejemplo, calcularemos el momento de inercia de un cilindro homogéneo con respecto a uno de sus ejes de simetría, el eje longitudinal z que pasa por su centro de masas. El elemento de volumen en este caso es el volumen de la corteza cilíndrica (representada en azul en la figura) de espesor dR que se encuentra a una distanciaR del eje de giro, y viene dado por:
 |
|
Sustituyendo en la expresión del momento de inercia:
 |
Integrando:
 |
Finalmente, sustituyendo la densidad en la expresión anterior, el momento de inercia del cilindro con respecto al eje z es:
 |
El momento de inercia de un cilindro hueco (con un radio interior R2, como se muestra en la siguiente figura), se calcula de la misma manera que el del cilindro macizo desarrollado en el ejemplo anterior, pero integrando entre R2 y R1).
 |
El momento de inercia de un cilindro hueco viene dado por:
 Conclusiones: |
Por tanto, a igual masa, un cilindro hueco tiene mayor momento de inercia que uno macizo. De su definición se deduce que el momento de inercia de un sólido depende del eje de giro (puesto que el radio de giro de cada partícula depende del eje).
Bibliografia:
lunes, 28 de noviembre de 2011
ESFUERZO Y DEFORMACION
ESFUERZO Y DEFORMACION
INTRODUCCIÓN
El diseño de cualquier elemento o de un sistema estructural implica responder dos preguntas: ¿El elemento es resistente a las cargas aplicadas? y ¿Tendrá la suficiente rigidez para que las deformaciones no sean excesivas e inadmisibles? Las respuestas a estas preguntas implican el análisis de la resistencia y rigidez de una estructura, aspectos que forman parte de sus requisitos. Estos análisis comienzan por la introducción de nuevos conceptos que son el esfuerzo y la deformación, aspectos que serán definidos a continuación (Salvadori y Heller, 1998; Timoshenko y Young, 2000).
Esfuerzo
σ = P/A
Donde:
P≡ Fuerza axial;
P≡ Fuerza axial;
A≡ Area de la sección transversal.
Cabe destacar que la fuerza empleada en la ec. 1 debe ser perpendicular al área analizada y aplicada en el centroide del área para así tener un valor de σ constante que se distribuye uniformemente en el área aplicada. La ec. 1 no es válida para los otros tipos de fuerzas internas1; existe otro tipo de ecuación que determine el esfuerzo para lasotras fuerzas, ya que los esfuerzos se distribuyen de otra forma.
Unidades
El esfuerzo utiliza unidades de fuerza sobre unidades de área, en el sistema internacional (SI) la fuerza es en Newton (N) y el área en metros cuadrados (m2), el esfuerzo se expresa por N/m2 o pascal (Pa). Esta unidad es pequeña por lo que se emplean múltiplos como el es el kilopascal (kPa), megapascal (MPa) o gigapascal (GPa). En el sistema americano, la fuerza es en libras y el área en pulgadas cuadradas, así el esfuerzo queda en libras sobre pulgadas cuadradas (psi). Particularmente en Venezuela la unidad más empleada es el kgf/cm2 para denotar los valores relacionados con el esfuerzo (Beer y Johnston, 1993; Popov, 1996; Singer y Pytel, 1982; Timoshenko y Young, 2000).
La resistencia del material no es el único parámetro que debe utilizarse al diseñar o analizar una estructura; controlar las deformaciones para que la estructura cumpla con el propósito para el cual se diseñó tiene la misma o mayor importancia. El análisis de las deformaciones se relaciona con los cambios en la forma de la estructura que generan las cargas aplicadas. 1 Fuerza cortante, momento flector y momento torsor.
Una barra sometida a una fuerza axial de tracción aumentara su longitud inicial; se puede observar que bajo la misma carga pero con una longitud mayor este aumento o alargamiento se incrementará también. Por ello definir la deformación (ε) como el cociente entre el alargamiento δ y la longitud inicial L, indica que sobre la barra la deformación es la misma porque si aumenta L también aumentaría δ. Matemáticamente la deformación sería:
ε =δ/L
Al observar la ec. 2 se obtiene que la deformación es un valor adimensional siendo el orden de magnitud en los casos del análisis estructural alrededor de 0,0012, lo cual es un valor pequeño (Beer y Johnston, 1993; Popov, 1996; Singer y Pytel, 1982).
DEFORMACIÓN ELÁSTICA
COMPORTAMIENTO ELASTICO Y PLASTICO
 Los diagramas esfuerzo – deformación unitaria reflejan el comportamiento de los materiales ingenieriles cuando se ensayan en tensión o en comprensión, como se describió en la sección anterior. Avanzando un paso más, consideramos lo que acontece cuando la carga se quita y el material se descarga.
Los diagramas esfuerzo – deformación unitaria reflejan el comportamiento de los materiales ingenieriles cuando se ensayan en tensión o en comprensión, como se describió en la sección anterior. Avanzando un paso más, consideramos lo que acontece cuando la carga se quita y el material se descarga.Por ejemplo, se aplica una carga a un espécimen de tensión, de tal modo que el esfuerzo y la deformación vayan desde el origen O hasta un punto A de la curva esfuerzo – deformación unitaria de la figura 1-18a. Además, supongamos que cuando se quita la carga, el material sigue exactamente la curva y regresa al origen O. Esta propiedad del material, por la que regresa a su dimensión original durante la descarga, se llama elasticidad y se dice que el material es elástico. Nótese que la curva esfuerzo – deformación unitaria no necesita ser lineal de O a A para que el material sea elástico.
Los diagramas esfuerzo – deformación unitaria que se describieron antes se obtuvieron en pruebas de tensión donde intervenían carga y descarga estática de las probetas, y en la descripción no entro el paso del tiempo. Sin embargo, cuando se cargan durante largos tiempos, algunos materiales desarrollan deformaciones adicionales y se dice que tienen flujo plástico o deformación gradual.
http://youtu.be/9AUjKHlWkU4
domingo, 27 de noviembre de 2011
DIAGRAMA ESFUERZO - DEFORMACIÓN UNITARIA
El diseño de elementos estructurales implica determinar la resistencia y rigidez del material estructural, estas propiedades se pueden relacionar si se evalúa una barra sometida a una fuerza axial para la cual se registra simultáneamente la fuerza aplicada y el alargamiento producido. Estos valores permiten determinar el esfuerzo y la deformación que al graficar originan el denominado diagrama de esfuerzo y deformación.
Los diagramas son similares si se trata del mismo material y de manera general permite agrupar los materiales dentro de dos categorías con propiedades afines que se denominan materiales dúctiles y materiales frágiles. Los diagramas de materiales dúctiles se caracterizan por ser capaces de resistir grandes deformaciones antes de la rotura, mientras que los frágiles presenta un alargamiento bajo cuando llegan al punto de rotura.
ESFUERZO.
Las fuerzas internas de un elemento están ubicadas dentro del material por lo que se distribuyen en toda el
área; justamente se denomina esfuerzo a la fuerza por unidad de área, la cual se denota con la letra griega sigma (σ) y
es un parámetro que permite comparar la resistencia de dos materiales, ya que establece una base común de
referencia.
σ = P/A
Donde:
P≡ Fuerza axial;
A≡ Area de la sección transversal
DEFORMACIÓN.
La resistencia del material no es el único parámetro que debe utilizarse al diseñar o analizar una estructura;
controlar las deformaciones para que la estructura cumpla con el propósito para el cual se diseñó tiene la misma o
mayor importancia.
El análisis de las deformaciones se relaciona con los cambios en la forma de la estructura que generan las cargas aplicadas. Una barra sometida a una fuerza axial de tracción aumentara su longitud inicial; se puede observar que bajo la misma carga pero con una longitud mayor este aumento o alargamiento se incrementará también. Por ello definir la deformación (ε) como el cociente entre el alargamiento δ y la longitud inicial L, indica que sobre la barra la deformación es la misma porque si aumenta L también aumentaría δ. Matemáticamente la deformación sería:
ε = δ/L
DIAGRAMA.
El diagrama es la curva resultante graficada con los valores del esfuerzo y la correspondiente deformación unitaria en el espécimen calculado a partir de los datos de un ensayo de tensión o de compresión.
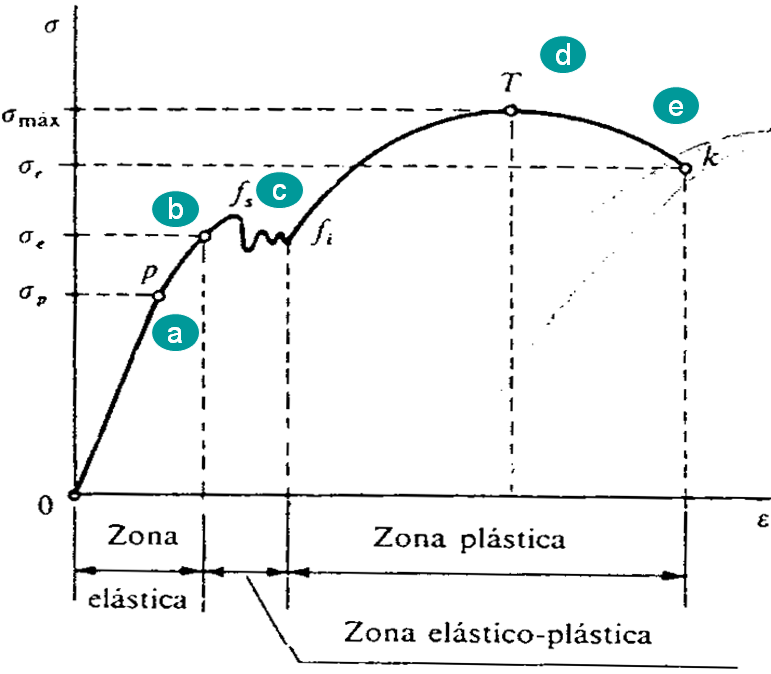
a) Límite de proporcionalidad:
Se observa que va desde el origen O hasta el punto llamado límite de proporcionalidad, es un segmento de recta rectilíneo, de donde se deduce la tan conocida relación de proporcionalidad entre la tensión y la deformación enunciada en el año 1678 por Robert Hooke. Cabe resaltar que, más allá la deformación deja de ser proporcional a la tensión.
b) Limite de elasticidad o limite elástico:
Es la tensión más allá del cual el material no recupera totalmente su forma original al ser descargado, sino que queda con una deformación residual llamada deformación permanente.
c) Punto de fluencia:
Es aquel donde en el aparece un considerable alargamiento o fluencia del material sin el correspondiente aumento de carga que, incluso, puede disminuir mientras dura la fluencia. Sin embargo, el fenómeno de la fluencia es característico del acero al carbono, mientras que hay otros tipos de aceros, aleaciones y otros metales y materiales diversos, en los que no manifiesta.
d) Esfuerzo máximo:
Es la máxima ordenada en la curva esfuerzo-deformación.
e) Esfuerzo de Rotura:
Verdadero esfuerzo generado en un material durante la rotura.
ZONA LASTICA - ZONA LASTICA Y ESFUERZO DE FLUENCIA
ZONA ELÁSTICA.
Es el área comprendida en un diagrama esfuerzo – deformación unitaria, por el trazo de la curva desde cero hasta el límite de elasticidad y por el valor de la abscisa, o sea la deformación correspondiente al limite elástico.
ZONA ELÁSTICA O LINEAL.
La zona elástica es reversible. La deformación elástica es una deformación temporal y se recupera totalmente cuando la carga es eliminada. El material absorbe energía elástica que después devuelve. Si no es así es porque hay histéresis. En esta zona se cumple la ley de Hooke , donde E es el módulo de Young. E mide la oposición que ejerce el material a ser deformado a tracción. Representa la rigidez del material. Se calcula experimentalmente de la gráfica.
Por ejemplo vamos a comparar módulos de Young de diferentes tipos de materiales medidos en GPa.
Por ejemplo vamos a comparar módulos de Young de diferentes tipos de materiales medidos en GPa.
- Metales: Acero 207 Aluminio 69 y Titanio 107
- Cerámicos: Vidrio 69 Alúmina 324
- Polímeros: Nailon 2.8 PVC 3.5 y Resina fenólica 6.5
La relación entre el esfuerzo y la deformación, denominada módulo de elasticidad, así como el límite de elasticidad, están determinados por la estructura molecular del material. La distancia entre las moléculas de un material no sometido a esfuerzo depende de un equilibrio entre las fuerzas moleculares de atracción y repulsión. Cuando se aplica una fuerza externa que crea una tensión en el interior del material, las distancias moleculares cambian y el material se deforma. Si las moléculas están firmemente unidas entre sí, la deformación no será muy grande incluso con un esfuerzo elevado. En cambio, si las moléculas están poco unidas, una tensión relativamente pequeña causará una deformación grande. Por debajo del límite de elasticidad, cuando se deja de aplicar la fuerza, las moléculas vuelven a su posición de equilibrio y el material elástico recupera su forma original. Más allá del límite de elasticidad, la fuerza aplicada separa tanto las moléculas que no pueden volver a su posición de partida, y el material queda permanentemente deformado o se rompe.
REFERENCIAS:
- Universidad Nacional de Trujillo
DEFORMACIÓN ELÁSTICA
Comportamiento bajo cargas Uniaxiales.
El grado con que una estructura se deforma depende de la magnitud de la tensión impuesta, para metales existe la relación: E=εσ. Esta es la llamada “LEY DE HOOKE”, donde:
σ : Tensión impuesta sobre un material.
ε : Deformación unitaria.
Cuando se tiene que la deformación es proporcional a la tensión, estamos en un caso denominado: Deformación Elástica, ésta no es permanente, lo cual significa que en cuanto se retire la fuerza de tensión, la pieza retoma su estado original, como apreciamos en el siguiente esquema: Si se aplica la carga, corresponde al movimiento desde el origen a lo largo de la recta, si se retira la carga (ocurre descarga) su dirección es opuesta, así vuelve al origen. Se hallan ciertos materiales, por ejemplo fundición gris y hormigón, para los cuales, el diagrama de tensión vs. La deformación no es lineal, en consecuencia, no es posible determinar el módulo elástico; entonces se habla de un Módulo Tangente o Módulo Secante.
- Módulo Tangente: Se toma como la pendiente de la curva tensión vs la deformación a algún determinado nivel de la tensión.
- Módulo Secante: Representa la pendiente trazada desde el origen hasta algún punto de la curva.
ANELASTICIDAD.
En la ingeniería de los materiales, existe una componente de la deformación elástica que depende del tiempo, es decir, la deformación elástica continúa aumentando después de aplicar la carga y para retirarla se requiere que haya transcurrido algún tiempo para que el material recupere su forma por completo.
Anelasticidad es el comportamiento elástico dependiente del tiempo que ocurre en un material y es causado por la dependencia del tiempo de los mecanismos.
ZONA PLÁSTICA.
Es el área comprendida en un diagrama esfuerzo- deformación unitaria, por el trazo de la curva desde el límite elástico hasta el punto de ruptura y por el tramo de la abscisa comprendida desde el valor del límite elástico y el valor correspondiente al punto de ruptura.
El equilibrio entre la fuerza aplicada y la deformidad inducida en un principio es lineal, la denominada como zona elástica (Fig. 1), si la deformación, y por tanto la fuerza continua, mantienen sus valores bajos. De persistir la fuerza se entra en una zona límite, denominada por los anglosajones como la "yield region", después de la cual, si la fuerza aumenta, se entra en la zona plástica, obviamente más rígida. De continuar aumentando el valor de la fuerza aplicada y no haber una adecuada respuesta de estrés, se produce el fallo catastrófico de la deformación, lo que ocasiona la rotura del objeto en cuestión.
- DEFORMACIÓN ELÁSTICA Y PLÁSTICA.
Un material sometido a una tensión (fuerza) produce una deformación del mismo. Si al cesar la fuerza el material vuelve a sus dimensiones primitivas, diremos que ha experimentado una deformación elástica. Si la deformación es tal que no recupera por completo sus medidas originales es una deformación plástica
- ZONA PLÁSTICA.
En el presente capítulo se consideran diferentes planteamientos para la estimación de la plasticidad en la punta de una grieta utilizando argumentos de la mecánica de la fractura elástica lineal (MFEL). Este es un aspecto relevante, ya que, debido a la singularidad del campo de tensiones en la punta de la grieta, es de esperar que siempre exista una zona de material cuyo comportamiento no se rige de acuerdo a los criterios de la elasticidad lineal. Aunque en capítulos posteriores se introducirán conceptos básicos de la mecánica de la fractura elastoplástica, antes de discutir dichas teorías es importante considerar distintas aproximaciones, propuestas a lo largo de los años, a fin de extender caracterizaciones basadas en el factor de intensidad de tensiones al caso de materiales “reales” que inevitablemente presentan cierta plasticidad en la punta de la grieta.
ESFUERZO DE FLUENCIA
Indicación del esfuerzo máximo que se puede desarrollar en un material sin causar una deformación plástica. Es el esfuerzo en el que un material exhibe una deformación permanente especificada y es una aproximación práctica de límite elástico. El límite elástico convencional está determinado a partir de un diagrama carga-deformación. Se trata del esfuerzo que corresponde a la intersección de la curva de carga-deformación y un paralelo de línea a la parte de la línea recta del diagrama por una deformación especificada. El desplazamiento de los metales suele especificarse como un 0,2%; es decir, la intersección de la línea de desplazamiento y el eje de esfuerzo 0 está en la deformación 0,2%. Normalmente, la deformación de los plásticos es el 2%.
Suscribirse a:
Entradas (Atom)












